RSM338: Machine Learning in Finance
Week 8: Nonlinear Classification | March 11–12, 2026
Rotman School of Management
Today’s Goal
Last week we learned about linear classification: LDA and logistic regression. These methods assume the decision boundary between classes is a straight line (or hyperplane).
The problem: In many real-world applications, the boundary between classes isn’t linear. Linear classifiers will struggle.
Today’s roadmap:
- Why linear fails: When classes aren’t linearly separable
- k-Nearest Neighbors: Let the data speak—classify based on similar observations
- Decision Trees: Partition the feature space with simple rules
- Information Gain: How trees decide where to split
- Application: Predicting loan defaults with the Lending Club dataset
Recap: Linear Classification
In Week 7, we saw that linear classifiers make predictions using:
\[z(\mathbf{x}) = w_0 + \mathbf{w}^\top \mathbf{x}\]
The class prediction depends on whether \(z(\mathbf{x})\) is positive or negative:
\[\hat{y} = \begin{cases} 1 & \text{if } z(\mathbf{x}) > 0 \\ 0 & \text{if } z(\mathbf{x}) \leq 0 \end{cases}\]
The decision boundary is where \(z(\mathbf{x}) = 0\)—a straight line in 2D, a plane in 3D, a hyperplane in higher dimensions.
Logistic regression transforms this into a probability using the sigmoid function, but the boundary is still linear.
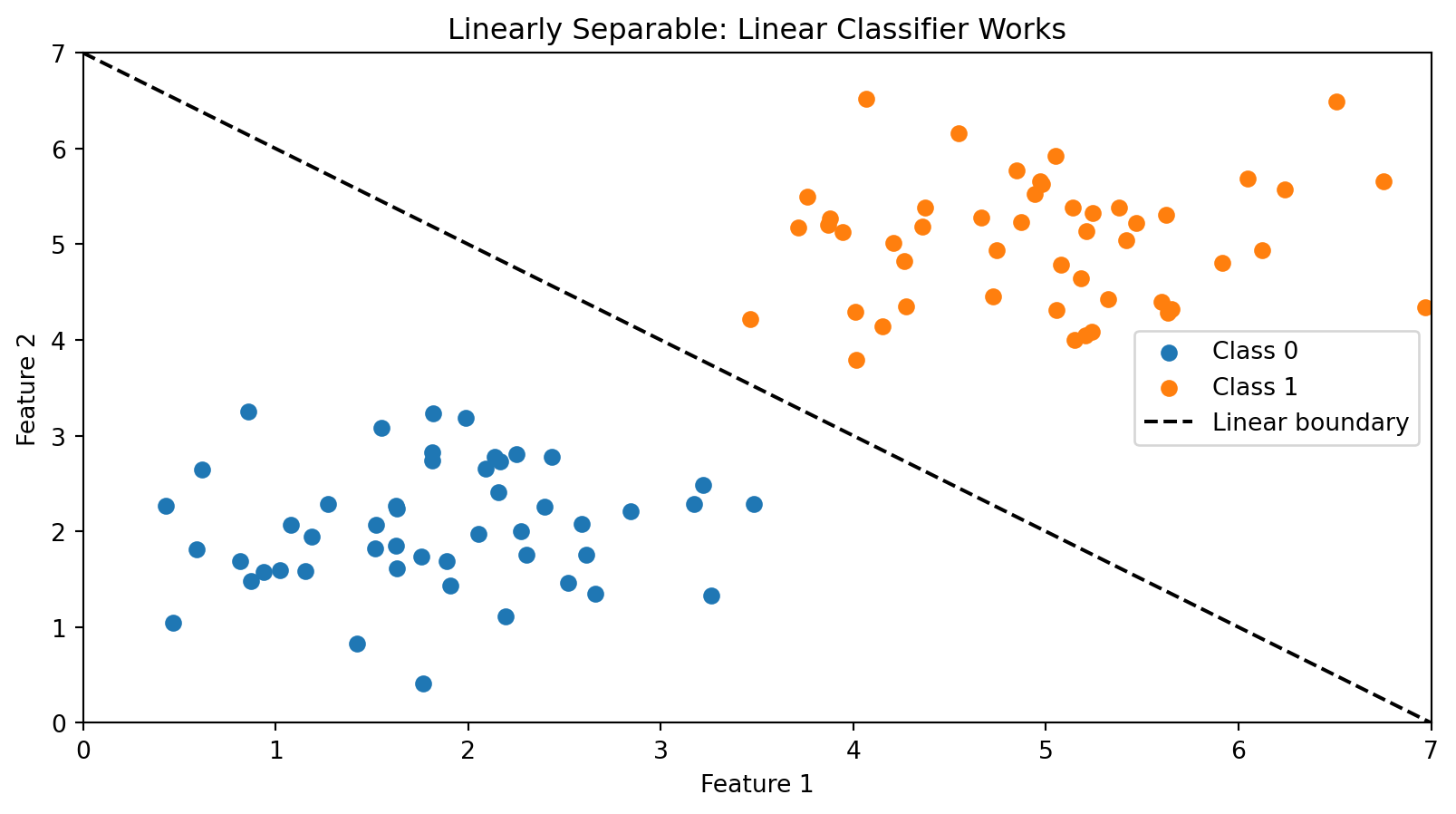
When Linear Classification Works
Linear classifiers work well when classes are linearly separable—you can draw a straight line between them.
A simple linear boundary perfectly separates the two classes.
The Feature Engineering Problem
Last week we saw that logistic regression can handle nonlinear boundaries if we add the right transformed features (e.g., \(x_1^2\), \(x_1 x_2\)). The model stays linear in its parameters — we just give it richer inputs.
But that approach has a big limitation: we have to know which transformations to use. With 2 features, adding squares and interactions is easy. With 50 features? There are 1,275 pairwise interactions and 50 squared terms — and we have no guarantee that quadratic terms are the right choice. Maybe the boundary depends on \(\log(x_3)\), or \(x_7 / x_{12}\), or something we’d never think to try.
We want methods that can learn nonlinear boundaries directly from the data, without us having to guess the right feature transformations in advance.
Classification in Finance: The Credit Default Problem
Consider a bank deciding whether to approve a loan. The outcome is binary:
- Class 1 (Default): The borrower fails to repay
- Class 0 (Repaid): The borrower repays in full
Based on features like credit score, income, and debt-to-income ratio, can we predict who will default?
The relationship between features and default is rarely linear. A borrower with moderate income and moderate credit score might default, while someone with either very high income OR very high credit score might not—this creates complex, non-linear boundaries.
Today we’ll learn two nonparametric methods that can capture these nonlinear patterns: k-Nearest Neighbors and Decision Trees.
Parametric vs. Nonparametric Models
Parametric models (like logistic regression) assume the data follows a specific functional form. We estimate a fixed set of parameters (\(w_0, w_1, \ldots, w_p\)), and these parameters define the model completely.
Nonparametric models make fewer assumptions about the functional form. Instead, they let the data determine the structure of the decision boundary.
| Parametric | Nonparametric | |
|---|---|---|
| Structure | Fixed form (e.g., linear) | Flexible, data-driven |
| Parameters | Fixed number | Grows with data |
| Examples | Logistic regression, LDA | k-NN, Decision Trees |
| Risk | Bias if form is wrong | Overfitting with limited data |
Both k-NN and decision trees are nonparametric—they don’t assume a linear (or any particular) decision boundary.
Part I: k-Nearest Neighbors
The Intuition Behind k-NN
k-Nearest Neighbors (k-NN) is based on a simple idea: similar observations should have similar outcomes.
To classify a new observation:
- Find the \(k\) training observations closest to it
- Take a vote among those \(k\) neighbors
- Assign the majority class
If you want to know if a new loan applicant will default, look at applicants in the training data who are most similar to them. If most of those similar applicants defaulted, predict default.
No training phase is needed—k-NN stores all the training data and does the work at prediction time. This is sometimes called a “lazy learner.”
Distance Recap (Week 4)
k-NN needs to measure how far apart two observations are. Same idea as clustering:
\[d(\mathbf{x}_i, \mathbf{x}_j) = \|\mathbf{x}_i - \mathbf{x}_j\| = \sqrt{\sum_{k=1}^{p} (x_{ik} - x_{jk})^2}\]
Two reminders from Week 4:
Standardize first. Features on different scales (income in dollars vs. DTI as a ratio) will make distance meaningless. Standardize each feature to mean 0, standard deviation 1.
Distance = norm of a difference. The \(L_2\) (Euclidean) norm is the default. Manhattan (\(L_1\)) is an alternative but Euclidean works well for most applications.
The k-NN Algorithm
Input: Training data \(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\), a new point \(\mathbf{x}\), and the number of neighbors \(k\).
Algorithm:
- Compute the distance from \(\mathbf{x}\) to every training observation \(\mathbf{x}_i\)
- Identify the \(k\) training observations with the smallest distances—call this set \(\mathcal{N}_k(\mathbf{x})\)
- Assign the class that appears most frequently among the \(k\) neighbors:
\[\hat{y} = \arg\max_c \sum_{i \in \mathcal{N}_k(\mathbf{x})} \unicode{x1D7D9}_{\{y_i = c\}}\]
The notation \(\unicode{x1D7D9}_{\{y_i = c\}}\) is the indicator function: it equals 1 if \(y_i = c\) and 0 otherwise. So we’re just counting votes.
k-NN in Action: k = 1
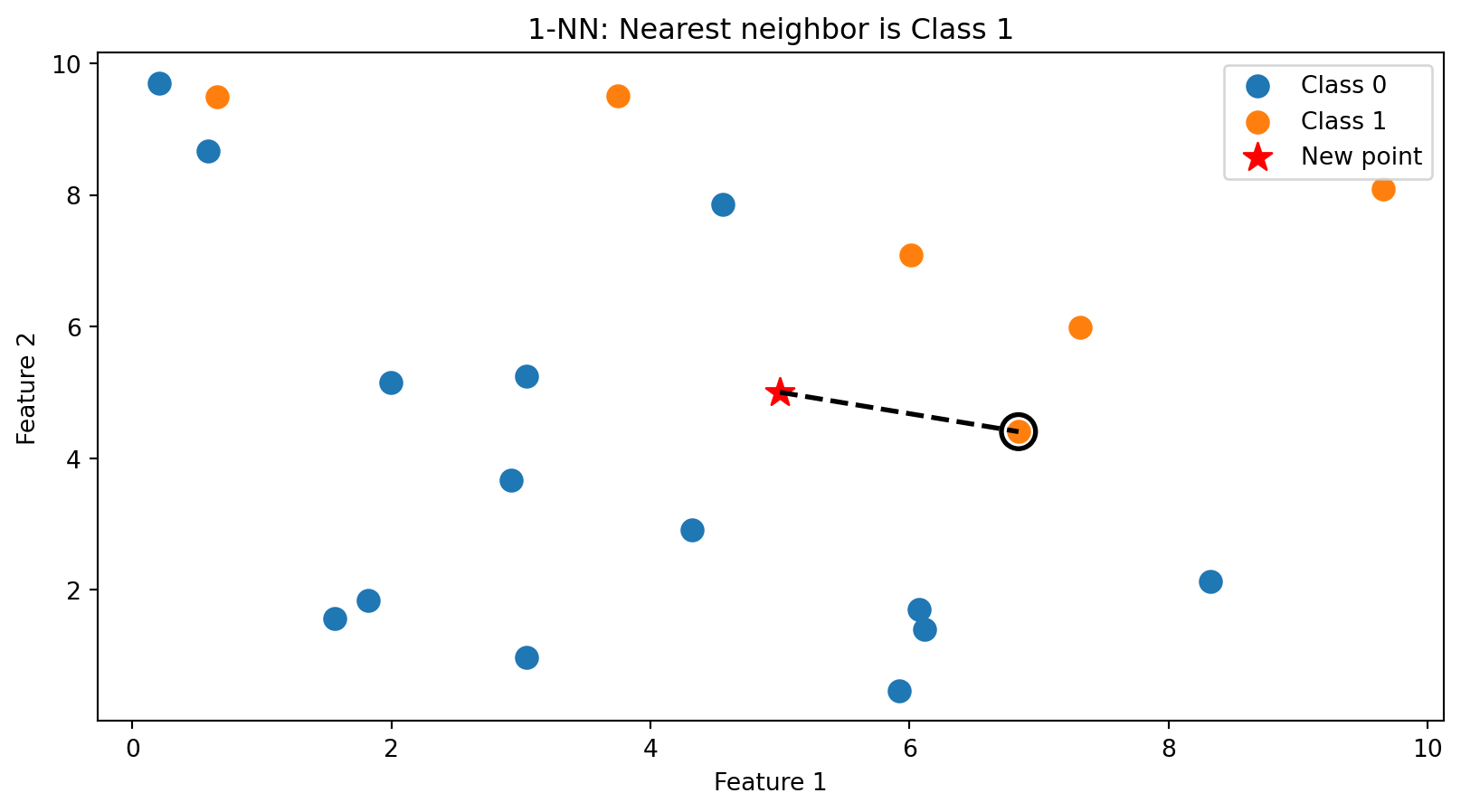
With \(k = 1\), we classify based on the single closest training point. The new point (star) is assigned the class of its nearest neighbor (circled).
k-NN in Action: k = 5
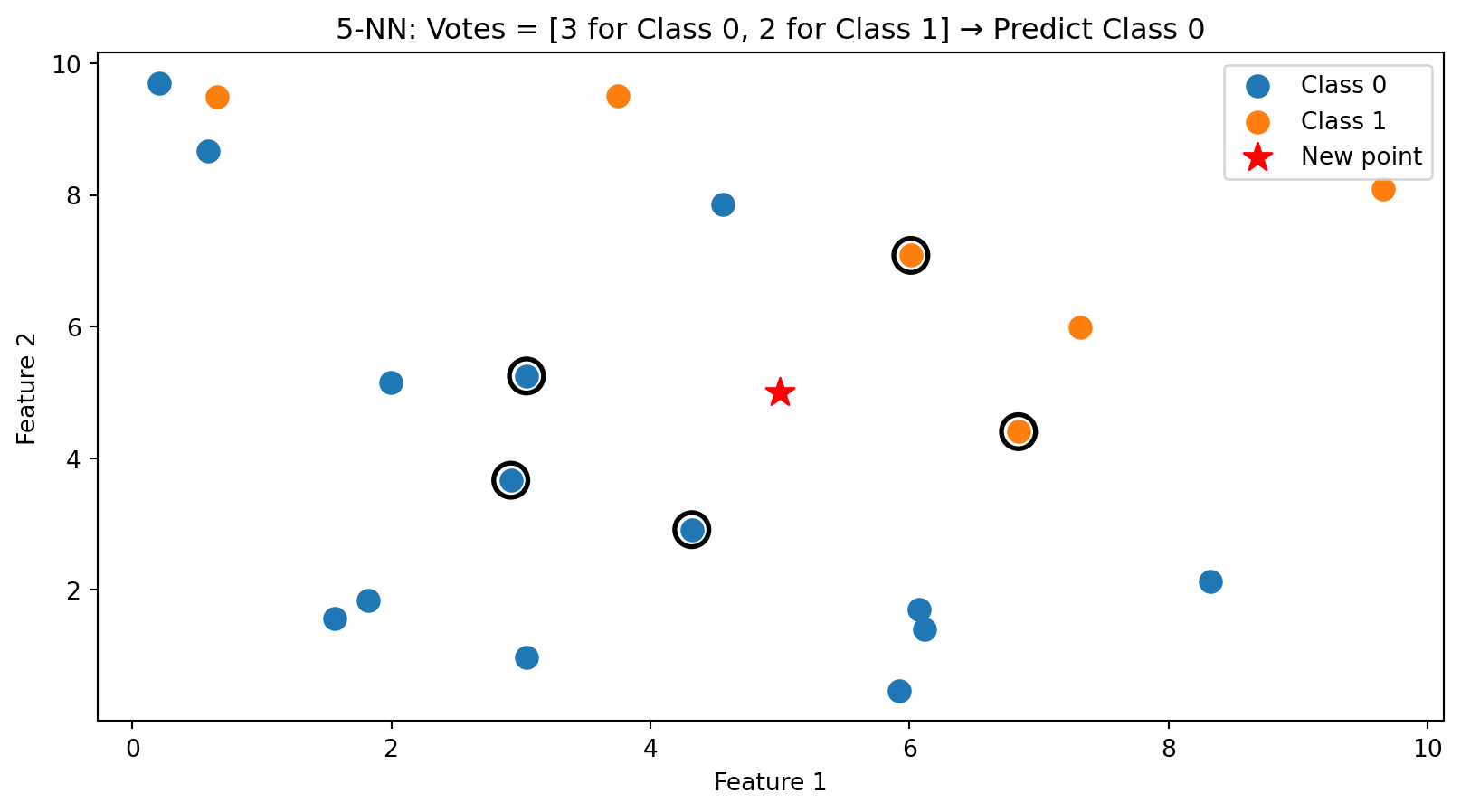
With \(k = 5\), we take a majority vote among the 5 nearest neighbors (circled). This is more robust than using just one neighbor.
The Decision Boundary of k-NN
Unlike linear classifiers, k-NN doesn’t explicitly compute a decision boundary. But we can visualize what the boundary looks like by classifying every point in the feature space.
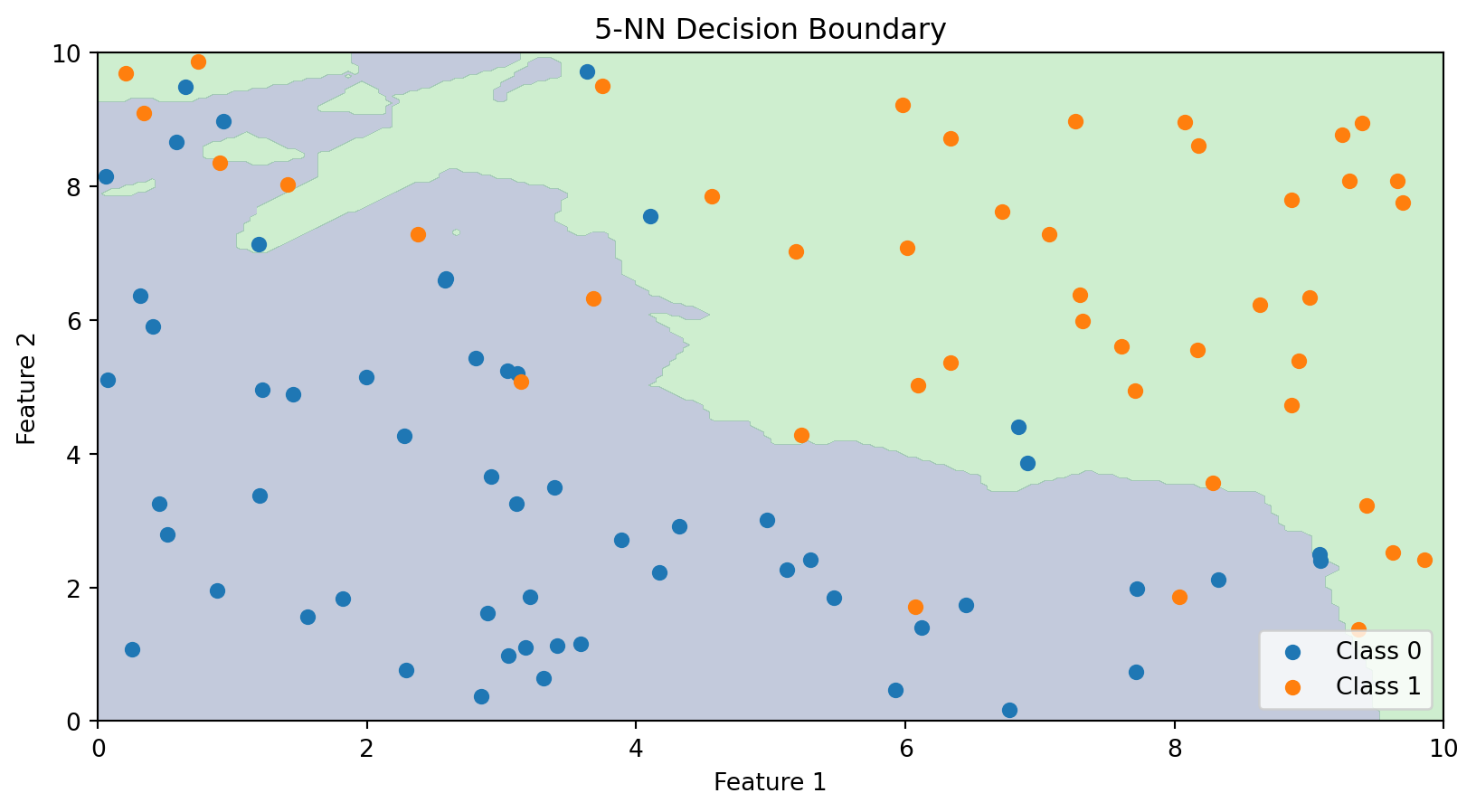
The k-NN decision boundary is nonlinear and adapts to the local density of data. It naturally forms complex shapes without us specifying any functional form.
The Role of k: Bias-Variance Tradeoff
The choice of \(k\) is crucial:
Small k (e.g., k = 1):
- Boundary closely follows the training data
- Very flexible—can capture complex patterns
- High variance, low bias
- Risk of overfitting (sensitive to noise)
Large k (e.g., k = 100):
- Boundary is smoother
- Less flexible—averages over many neighbors
- Low variance, high bias
- Risk of underfitting (misses local patterns)
This is the bias-variance tradeoff we’ve seen before. We need to choose \(k\) that balances these concerns.
Effect of k on the Decision Boundary
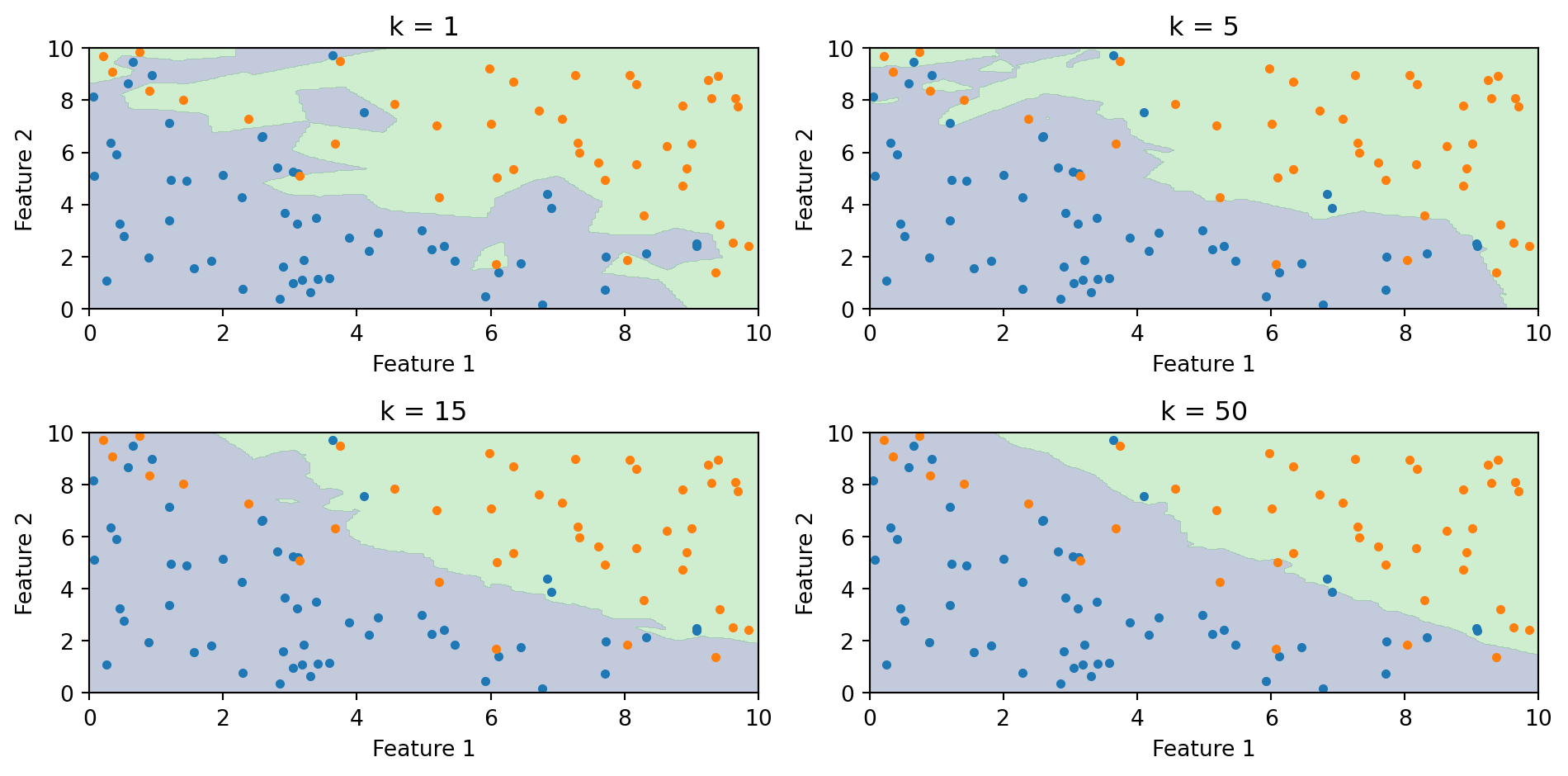
As \(k\) increases, the boundary becomes smoother. With \(k = 1\), every training point gets its own region. With large \(k\), the boundary approaches the overall majority class.
Choosing k with Cross-Validation
How do we choose \(k\)? Use cross-validation (from Week 5):
- Split training data into folds
- For each candidate value of \(k\):
- Fit k-NN on training folds
- Evaluate accuracy on validation fold
- Choose \(k\) that maximizes cross-validated accuracy
A common rule of thumb: \(k < \sqrt{n}\) where \(n\) is the sample size. But cross-validation is more reliable.
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
import numpy as np
# Try different values of k
k_values = range(1, 31)
cv_scores = []
for k in k_values:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X_train, y_train, cv=5)
cv_scores.append(scores.mean())
best_k = k_values[np.argmax(cv_scores)]
print(f"Best k: {best_k} with CV accuracy: {max(cv_scores):.3f}")Best k: 19 with CV accuracy: 0.850k-NN: Advantages and Disadvantages
Advantages:
- Simple to understand and implement
- No training phase (just store the data)
- Naturally handles multi-class problems
- Can capture complex, nonlinear boundaries
- No assumptions about the data distribution
Disadvantages:
- Slow at prediction time—must compute distances to all training points
- Doesn’t work well in high dimensions (“curse of dimensionality”)
- Sensitive to irrelevant features (all features contribute to distance)
- Requires feature scaling
For large datasets, approximate nearest neighbor methods can speed up k-NN, but it remains computationally intensive.
The Curse of Dimensionality
k-NN relies on distance, and distance breaks down in high dimensions. Three related problems:
The space becomes sparse. In 1D, 100 points cover the range well. In 2D, the same 100 points are scattered across a plane. In 50D, they’re lost in a vast empty space. The amount of data you need to “fill” the space grows exponentially with \(p\).
You need more data to have local neighbours. If the space is mostly empty, the \(k\) “nearest” neighbours may be far away — and far-away neighbours aren’t informative about the local structure.
Distances become less informative. Euclidean distance sums \(p\) squared differences. As \(p\) grows, all these sums converge to roughly the same value (law of large numbers). The nearest and farthest neighbours end up almost the same distance away, so “nearest” stops meaning much.
Part II: Decision Trees
The Intuition Behind Decision Trees
Decision trees mimic how humans make decisions: a series of yes/no questions.
Consider a loan officer evaluating an application:
- Is the credit score above 700?
- If no → High risk, deny
- If yes → Continue…
- Is the debt-to-income ratio below 35%?
- If no → Medium risk, deny
- If yes → Low risk, approve
Each question splits the population into subgroups, and we make predictions based on which group an observation falls into.
Decision trees automate this process: they learn which questions to ask and in what order.
Anatomy of a Decision Tree
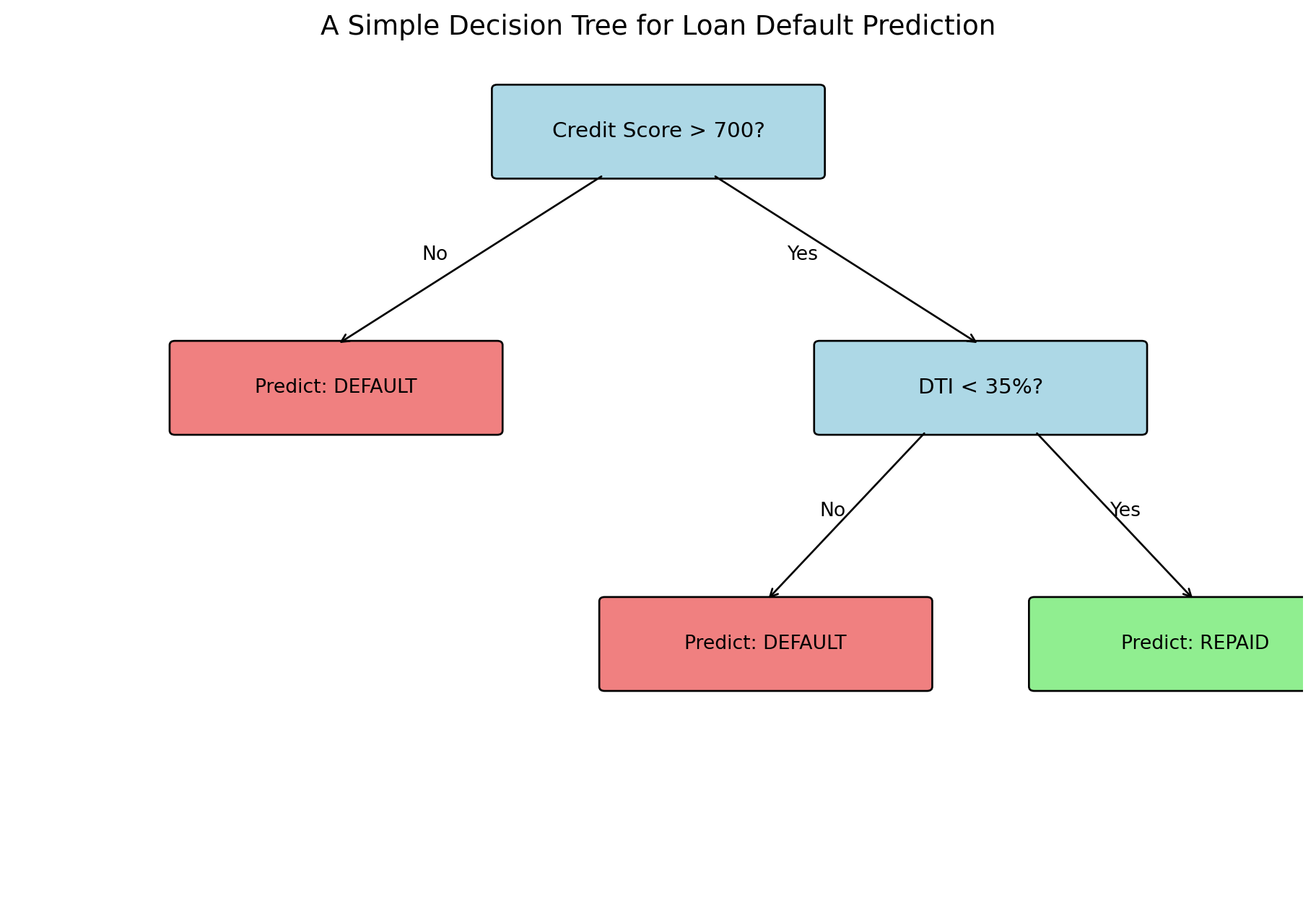
Terminology:
- Root node: The first split (top of the tree)
- Internal nodes: Decision points that split the data
- Leaf nodes: Terminal nodes that make predictions
- Depth: The number of splits from root to leaf
How Trees Partition the Feature Space
Each split in a decision tree divides the feature space with an axis-aligned boundary (parallel to one axis).
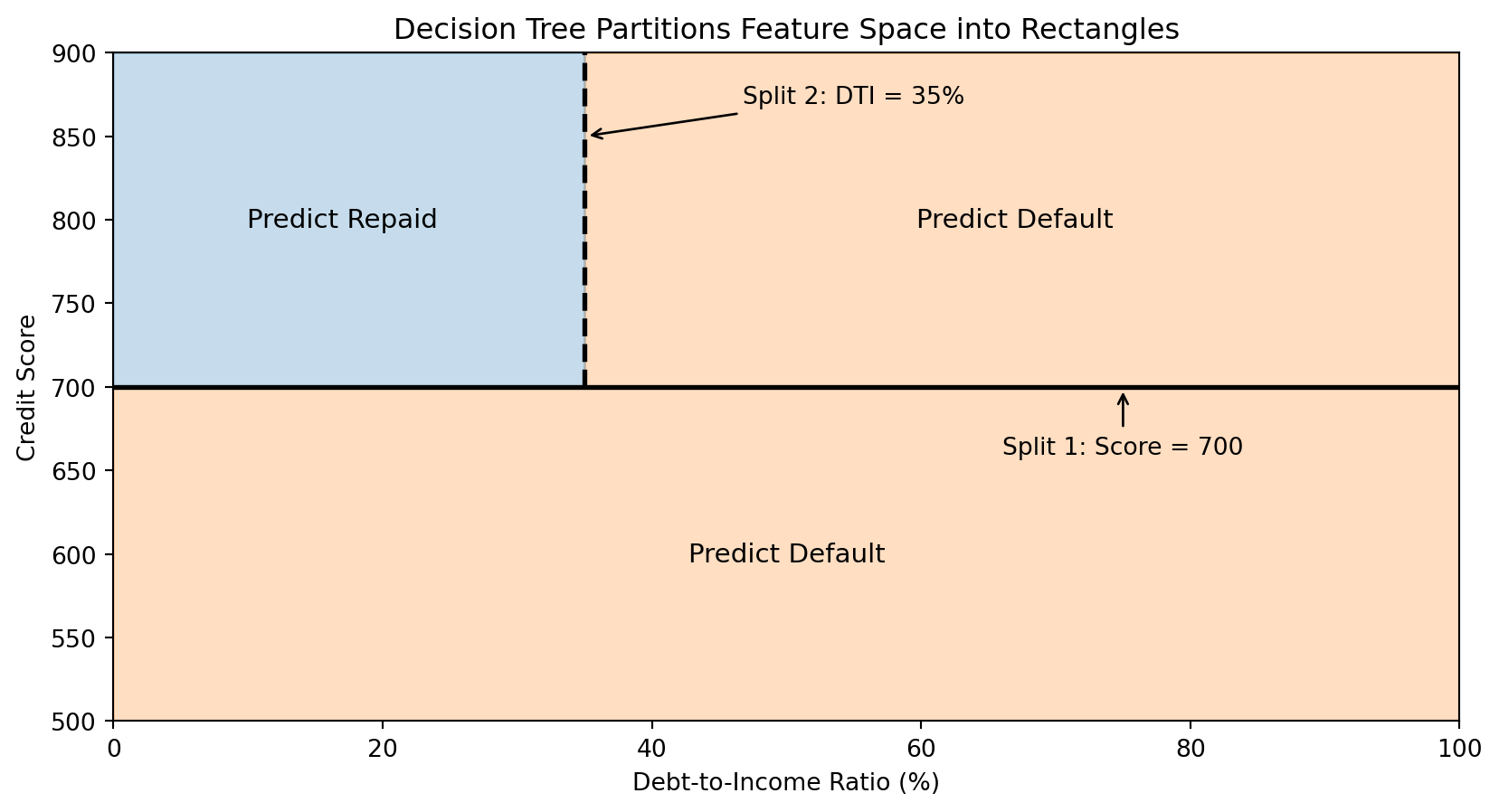
The tree creates rectangular regions. Each leaf corresponds to one region, and all observations in that region get the same prediction.
The Decision Tree Algorithm: Recursive Partitioning
The Goal: Build a tree that makes good predictions.
The Approach: Greedy, recursive partitioning.
- Start with all training data at the root
- Find the best split—the feature and threshold that best separates the classes
- Split the data into two groups based on this rule
- Recursively apply steps 2-3 to each group
- Stop when a stopping criterion is met (e.g., minimum samples per leaf, maximum depth)
The key question: How do we define “best” split?
Measuring Split Quality: Impurity
A good split should create child nodes that are more “pure” than the parent—ideally, each child contains only one class.
We measure impurity—how mixed the classes are in a node. A pure node (all one class) has impurity = 0.
For a node with \(n\) observations where \(p_c\) is the proportion belonging to class \(c\):
Gini impurity: \[\text{Gini} = 1 - \sum_c p_c^2\]
Entropy: \[\text{Entropy} = -\sum_c p_c \log_2(p_c)\]
Both measures equal 0 for a pure node and are maximized when classes are equally mixed.
Understanding Gini Impurity
For binary classification with \(p\) being the proportion in class 1:
\[\text{Gini} = 1 - p^2 - (1-p)^2 = 2p(1-p)\]
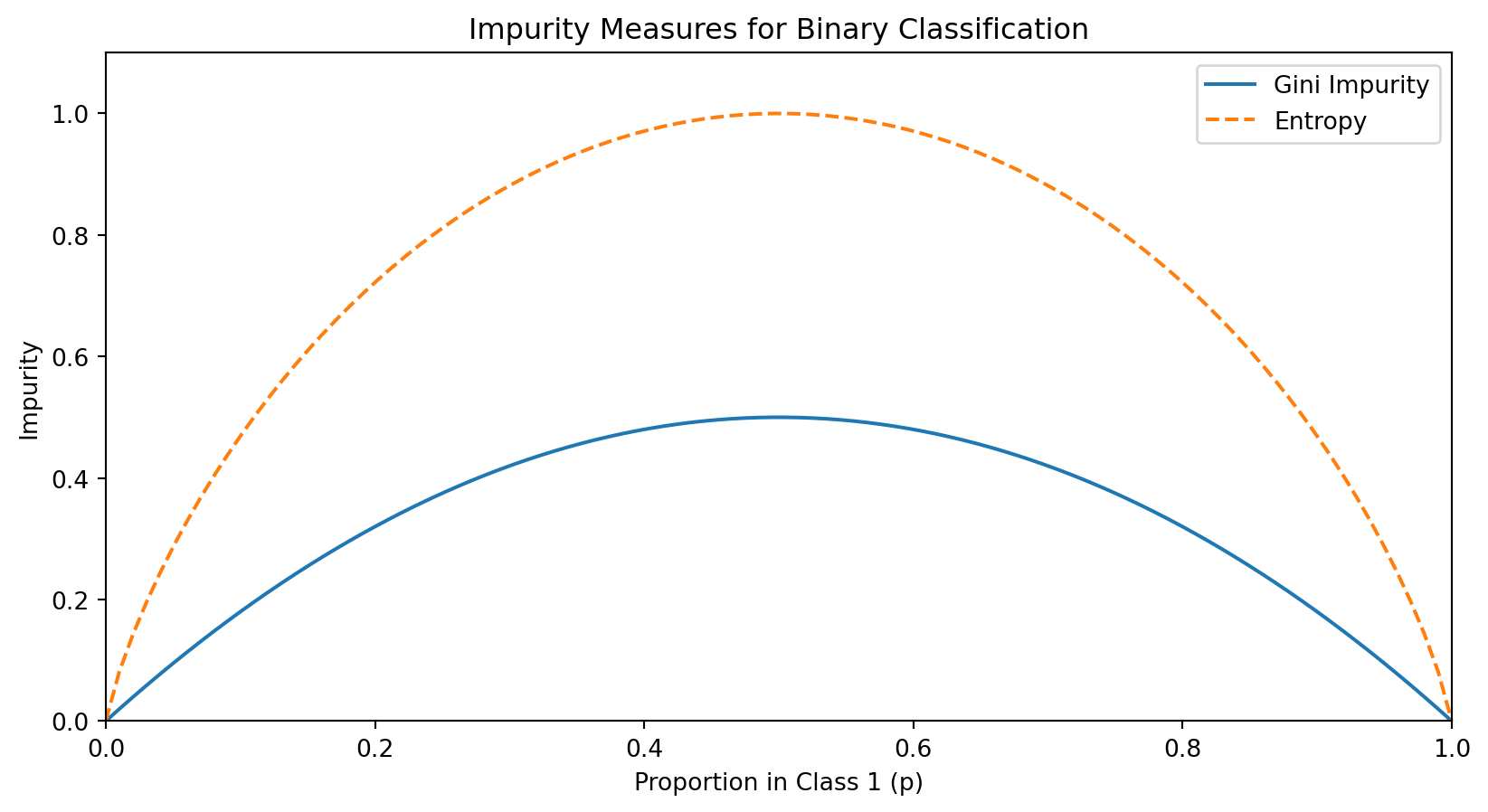
Both measures are minimized (= 0) when \(p = 0\) or \(p = 1\) (pure node) and maximized when \(p = 0.5\) (maximum uncertainty).
Computing Information Gain
Information gain measures how much a split reduces impurity.
If a parent node \(P\) is split into children \(L\) (left) and \(R\) (right):
\[\text{Information Gain} = \text{Impurity}(P) - \left[\frac{n_L}{n_P} \cdot \text{Impurity}(L) + \frac{n_R}{n_P} \cdot \text{Impurity}(R)\right]\]
where \(n_P\), \(n_L\), \(n_R\) are the number of observations in the parent, left child, and right child.
The weighted average accounts for the sizes of the child nodes. The best split is the one that maximizes information gain.
Example: Computing Information Gain
Suppose we have 100 loan applicants: 60 repaid, 40 defaulted.
Parent impurity (Gini): \[\text{Gini}_P = 1 - (0.6)^2 - (0.4)^2 = 1 - 0.36 - 0.16 = 0.48\]
Option A: Split on Credit Score > 700
- Left (below 700): 30 observations (10 repaid, 20 default) → Gini = \(1 - (1/3)^2 - (2/3)^2 = 0.444\)
- Right (above 700): 70 observations (50 repaid, 20 default) → Gini = \(1 - (5/7)^2 - (2/7)^2 = 0.408\)
\[\text{Gain}_A = 0.48 - \left[\frac{30}{100}(0.444) + \frac{70}{100}(0.408)\right] = 0.48 - 0.419 = 0.061\]
We’d compute this for all possible features and thresholds, then choose the split with highest gain.
For Continuous Features: Finding the Best Threshold
For a continuous feature (like credit score), we need to find the best threshold for splitting.
Algorithm:
- Sort the observations by the feature value
- Consider each unique value as a potential threshold
- For each threshold, compute the information gain
- Choose the threshold with the highest gain
If there are \(n\) unique values, we evaluate up to \(n-1\) possible splits for that feature. This is computationally tractable because we can update class counts incrementally as we move through sorted values.
Building a Tree in Python
from sklearn.tree import DecisionTreeClassifier
import numpy as np
# Generate sample data
np.random.seed(42)
n = 200
credit_score = np.random.normal(700, 50, n)
dti = np.random.normal(30, 10, n)
X = np.column_stack([credit_score, dti])
# Default probability depends on both features
prob_default = 1 / (1 + np.exp(0.02 * (credit_score - 680) - 0.05 * (dti - 35)))
y = (np.random.random(n) < prob_default).astype(int)
# Fit decision tree
tree = DecisionTreeClassifier(max_depth=3, random_state=42)
tree.fit(X, y)
print(f"Tree depth: {tree.get_depth()}")
print(f"Number of leaves: {tree.get_n_leaves()}")
print(f"Training accuracy: {tree.score(X, y):.3f}")Tree depth: 3
Number of leaves: 8
Training accuracy: 0.720Visualizing the Learned Tree
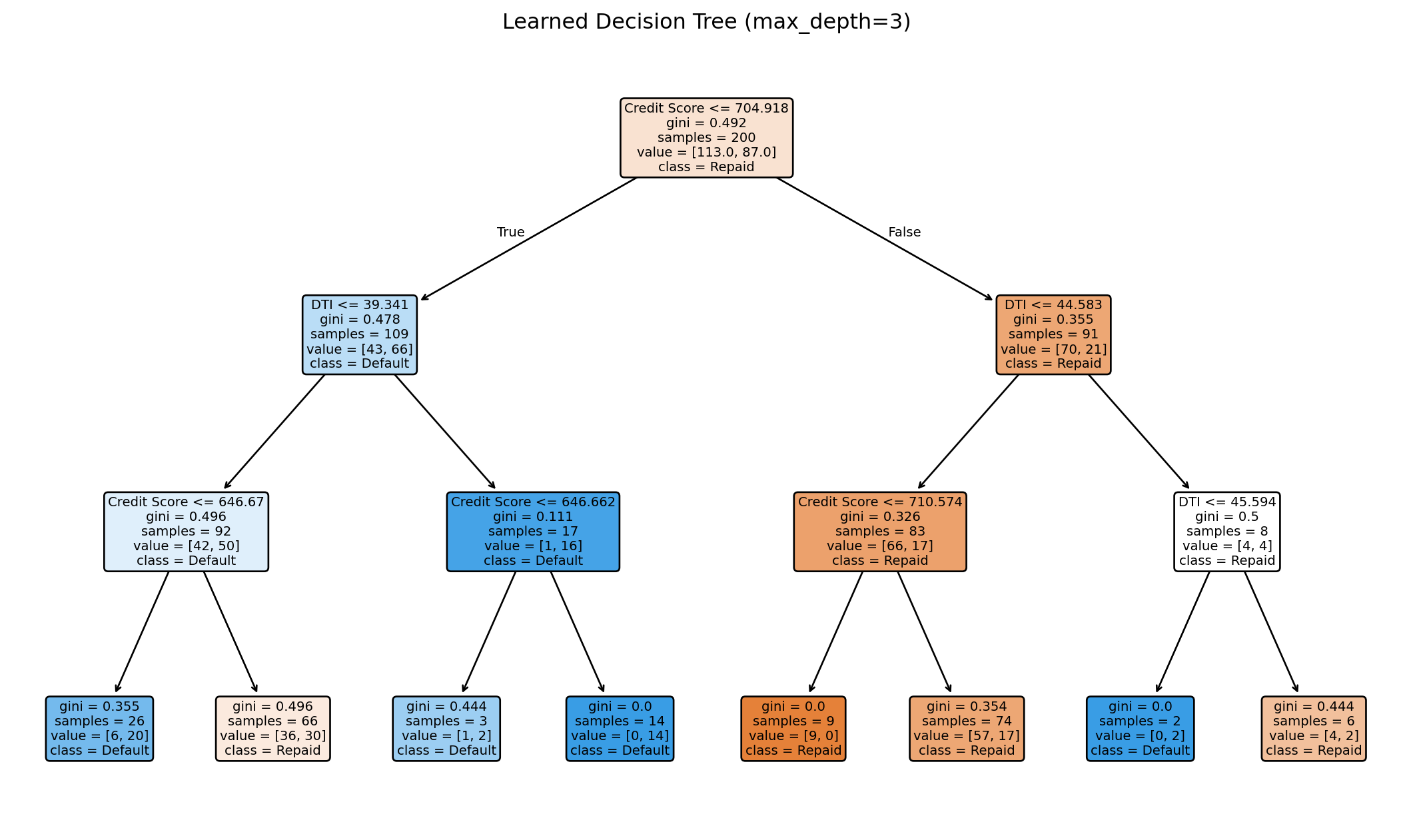
The tree learns splits automatically from the data. Each node shows the split condition, impurity, sample count, and class distribution.
The Decision Boundary of a Tree
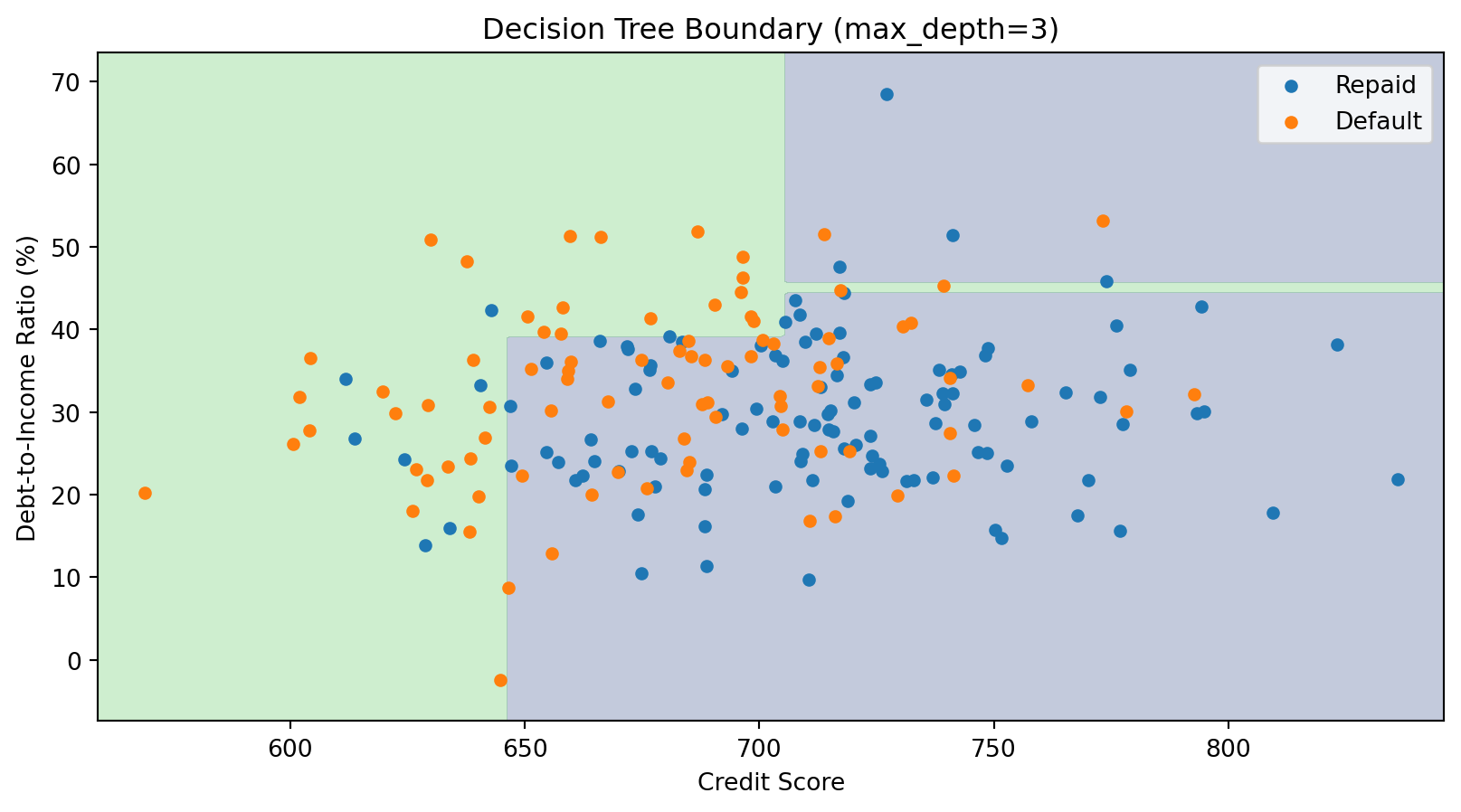
Decision tree boundaries are always axis-aligned rectangles—combinations of horizontal and vertical lines. This is a limitation compared to k-NN’s curved boundaries.
Controlling Tree Complexity
Deep trees can overfit—they memorize the training data perfectly but fail on new data.
Strategies to prevent overfitting:
- Pre-pruning: Stop growing before the tree becomes too complex
max_depth: Maximum tree depthmin_samples_split: Minimum samples required to split a nodemin_samples_leaf: Minimum samples required in a leaf
- Post-pruning: Grow a full tree, then remove branches that don’t help
ccp_alpha: Cost-complexity pruning parameter
These hyperparameters are chosen via cross-validation.
Effect of Tree Depth
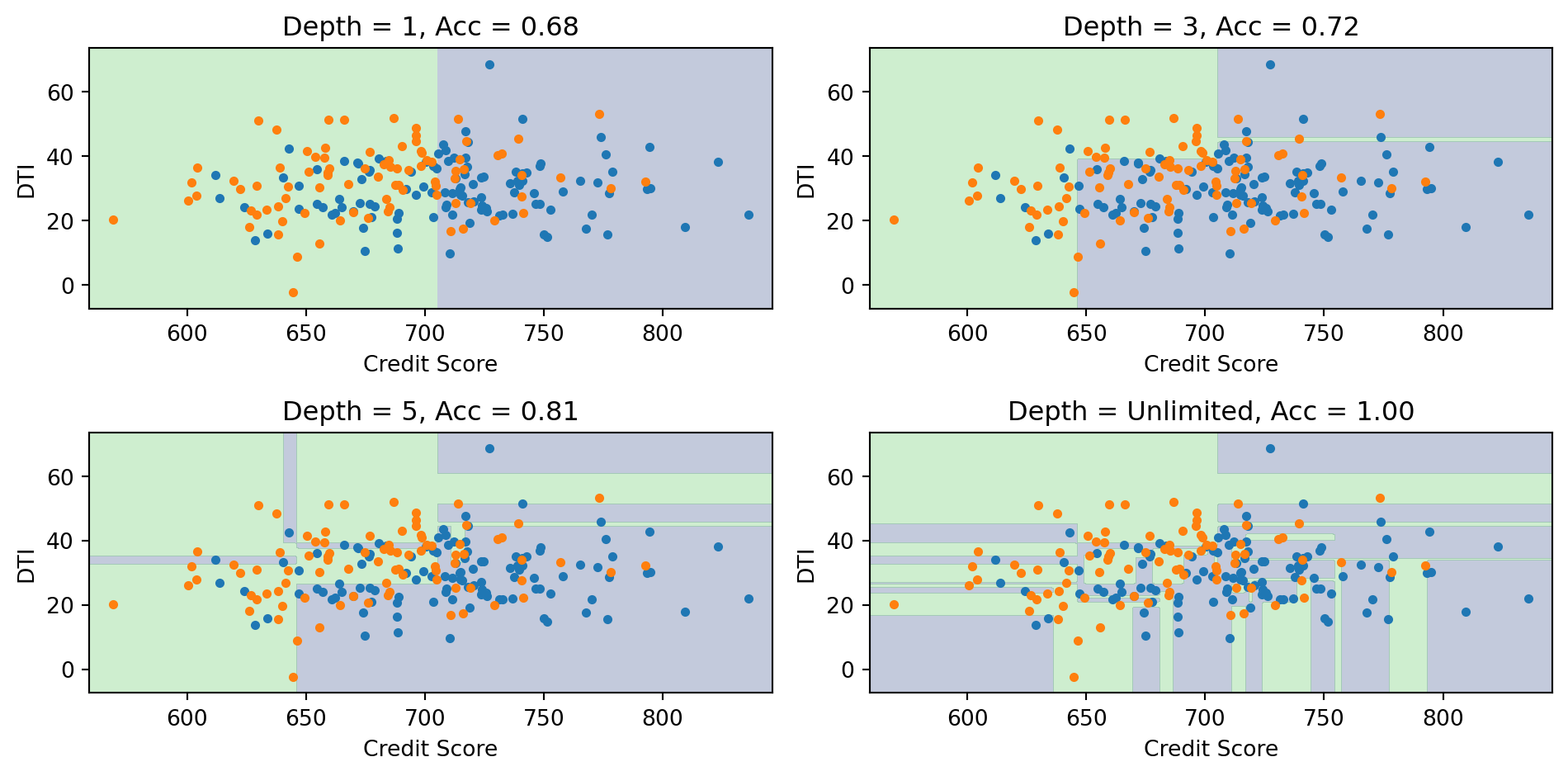
Deeper trees create more complex boundaries. With unlimited depth, the tree can achieve 100% training accuracy but likely overfits.
Decision Trees: Advantages and Disadvantages
Advantages:
- Easy to interpret and explain (white-box model)
- Handles both numeric and categorical features
- Requires little data preprocessing (no scaling needed)
- Can capture interactions between features
- Fast prediction
Disadvantages:
- Axis-aligned boundaries only (can’t capture diagonal boundaries efficiently)
- High variance—small changes in data can produce very different trees
- Prone to overfitting without regularization
- Greedy algorithm may not find globally optimal tree
The high variance problem is addressed by ensemble methods (Random Forests, Gradient Boosting)—we’ll cover these in Week 9.
Part III: Comparing k-NN and Decision Trees
k-NN vs. Decision Trees
| Aspect | k-NN | Decision Trees |
|---|---|---|
| Decision boundary | Flexible, curved | Axis-aligned rectangles |
| Training | None (stores data) | Builds tree structure |
| Prediction speed | Slow (compare to all training) | Fast (traverse tree) |
| Interpretability | Low (black-box) | High (rules) |
| Feature scaling | Required | Not required |
| High dimensions | Struggles (curse of dim.) | Handles better |
| Missing data | Problematic | Can handle |
Neither method dominates—the best choice depends on the data and application requirements.
When to Use k-NN
k-NN is a good choice when:
- You have low to moderate dimensionality (say, \(p < 20\))
- The decision boundary is expected to be complex and curved
- Interpretability is not critical
- You have enough computational resources for prediction
- The data is relatively dense
Applications in finance:
- Anomaly detection (fraudulent transactions look different from neighbors)
- Collaborative filtering (recommend assets held by similar investors)
- Pattern matching (find historical periods similar to current conditions)
When to Use Decision Trees
Decision trees are a good choice when:
- Interpretability is important (need to explain decisions)
- You have mixed feature types (numeric and categorical)
- There may be complex interactions between features
- Fast prediction is required
- You’ll use them as building blocks for ensembles
Applications in finance:
- Credit scoring (need explainable decisions for regulatory compliance)
- Customer segmentation (identify distinct client groups)
- Risk management (clear rules for risk categories)
Part IV: Application to Lending Club Data
The Lending Club Dataset
Lending Club was a peer-to-peer lending platform where individuals could lend money to other individuals.
The classification problem: Given borrower characteristics at the time of application, predict whether the loan will be repaid or will default.
Features include:
- FICO score (credit score, 300-850)
- Annual income
- Debt-to-income ratio (DTI)
- Home ownership (own, mortgage, rent)
- Loan amount
- Employment length
This is a real business problem with significant financial stakes—approving a bad loan costs money, but rejecting a good loan loses revenue.
Loading and Preparing the Data
import pandas as pd
# Load Lending Club data (pre-split by Hull)
train_data = pd.read_excel('lendingclub_traindata.xlsx')
test_data = pd.read_excel('lendingclub_testdata.xlsx')
# Check columns and target
print(f"Training samples: {len(train_data)}")
print(f"Test samples: {len(test_data)}")
print(f"\nTarget distribution in training data:")
print(train_data['loan_status'].value_counts(normalize=True))Training samples: 8695
Test samples: 5916
Target distribution in training data:
loan_status
1 0.827602
0 0.172398
Name: proportion, dtype: float64Class Imbalance
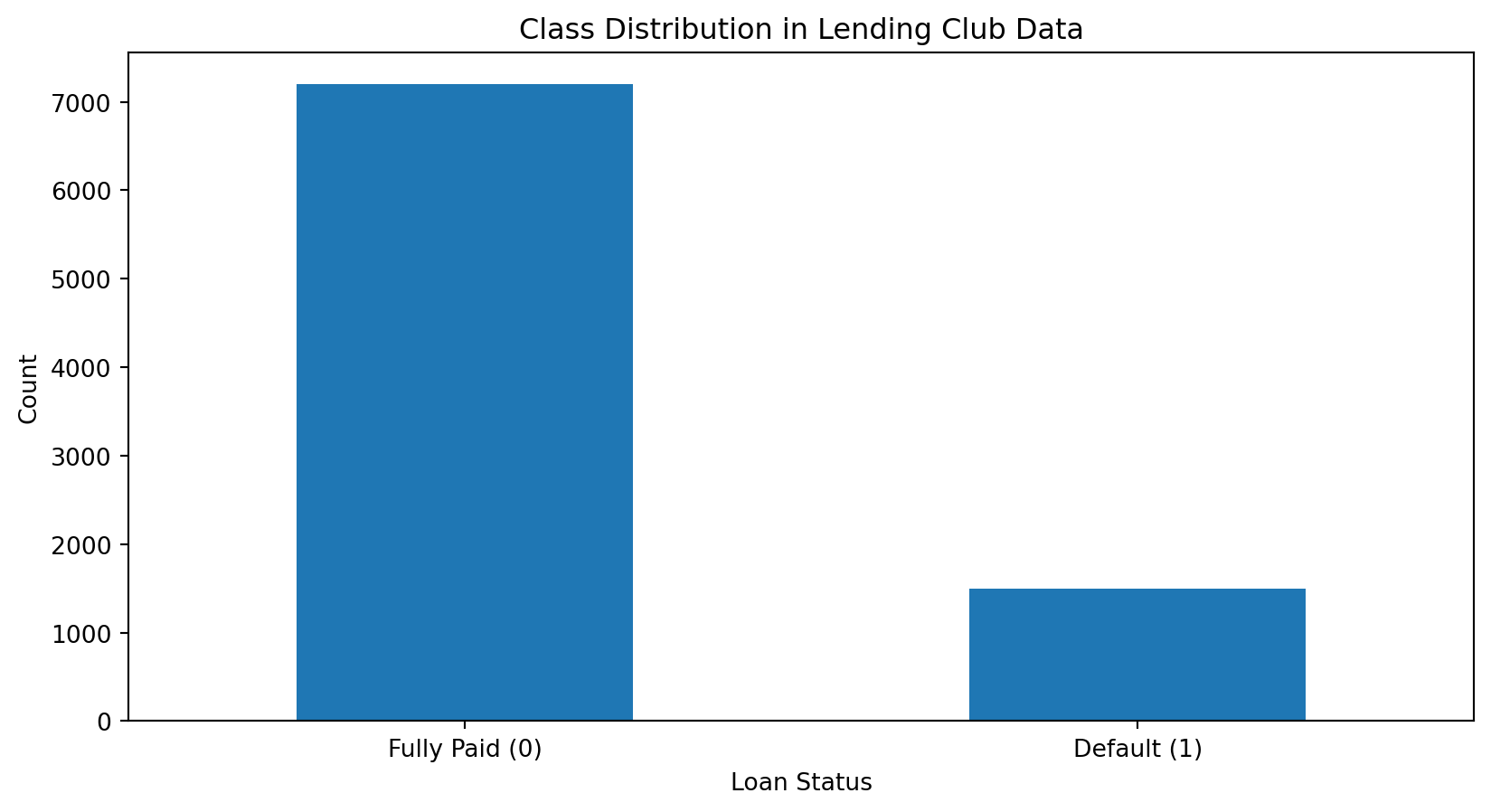
Fully paid: 17.2%
Default: 82.8%The data is imbalanced: most loans are repaid. This is realistic—lenders wouldn’t survive if most loans defaulted!
Imbalanced data requires careful evaluation. High accuracy might just mean predicting “repaid” for everyone.
Preparing Features
# Select features for modeling
features = ['fico_low', 'income', 'dti', 'home_ownership']
# Prepare X and y
X_train = train_data[features].copy()
y_train = train_data['loan_status'].values
X_test = test_data[features].copy()
y_test = test_data['loan_status'].values
# Handle missing values if any
X_train = X_train.fillna(X_train.median())
X_test = X_test.fillna(X_train.median())
print(f"\nFeature summary:")
print(X_train.describe())
Feature summary:
fico_low income dti home_ownership
count 8695.000000 8695.000000 8695.000000 8695.000000
mean 694.542841 77.871491 19.512814 0.591374
std 30.393493 57.737053 16.928800 0.491608
min 660.000000 0.200000 0.000000 0.000000
25% 670.000000 46.374000 12.800000 0.000000
50% 685.000000 65.000000 18.630000 1.000000
75% 710.000000 93.000000 25.100000 1.000000
max 845.000000 1500.000000 999.000000 1.000000Training k-NN
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score
# Scale features for k-NN
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Find best k using cross-validation
k_values = range(1, 101, 5)
cv_scores = []
for k in k_values:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X_train_scaled, y_train, cv=5, scoring='roc_auc')
cv_scores.append(scores.mean())
# print(f"k = {k}: CV AUC = {scores.mean():.4f} (+/- {scores.std():.4f})")
best_k = list(k_values)[cv_scores.index(max(cv_scores))]
print(f"Best k: {best_k} (CV AUC = {max(cv_scores):.4f})")Best k: 91 (CV AUC = 0.6004)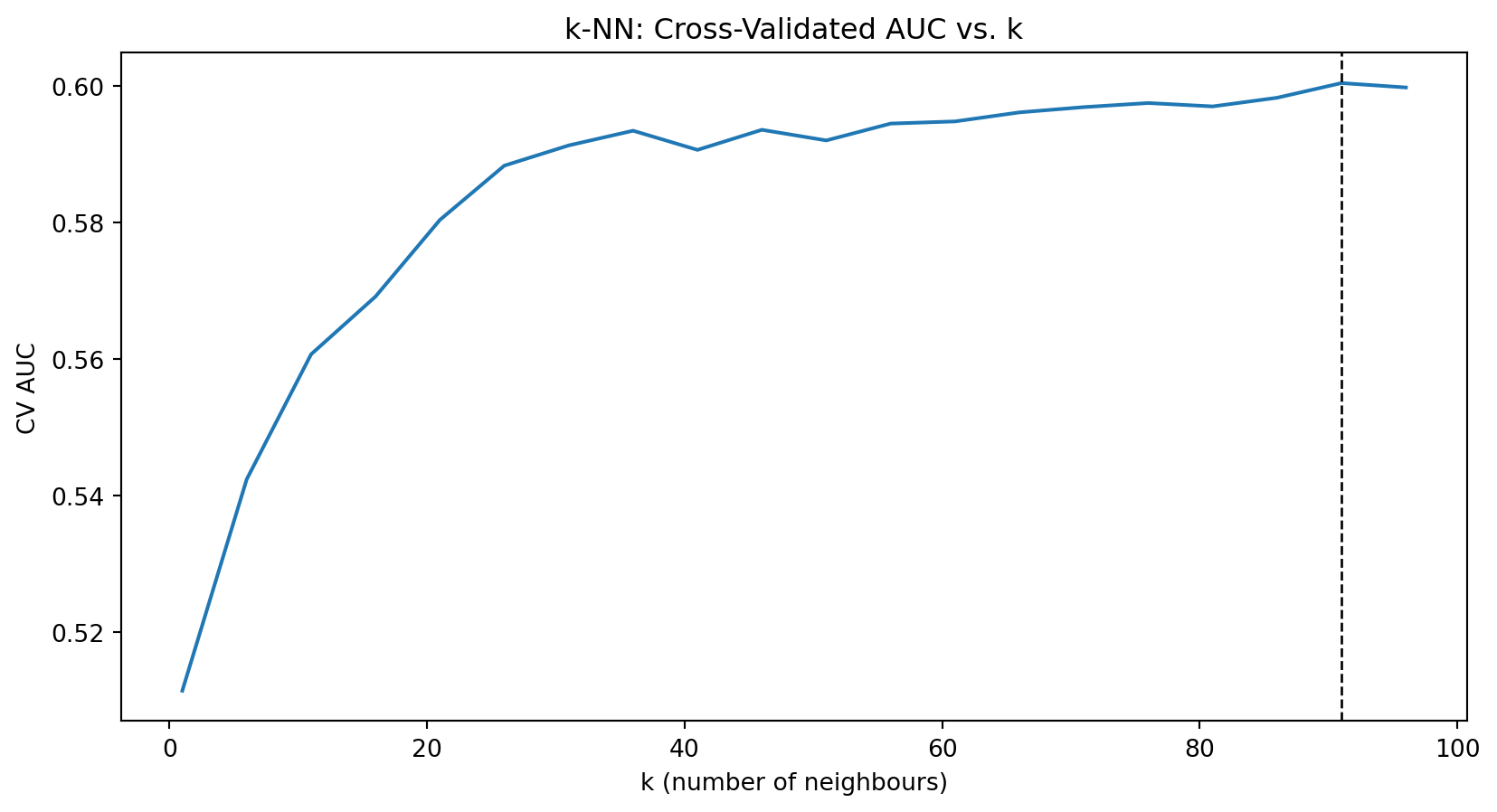
Training a Decision Tree
from sklearn.tree import DecisionTreeClassifier
# Find best max_depth using cross-validation
depths = [2, 3, 4, 5, 6, 7, 8]
cv_scores_tree = []
for depth in depths:
tree = DecisionTreeClassifier(max_depth=depth, random_state=42)
scores = cross_val_score(tree, X_train, y_train, cv=5, scoring='roc_auc')
cv_scores_tree.append(scores.mean())
print(f"depth = {depth}: CV AUC = {scores.mean():.4f} (+/- {scores.std():.4f})")
best_depth = depths[cv_scores_tree.index(max(cv_scores_tree))]
print(f"\nBest max_depth: {best_depth}")depth = 2: CV AUC = 0.5749 (+/- 0.0156)
depth = 3: CV AUC = 0.5867 (+/- 0.0129)
depth = 4: CV AUC = 0.5902 (+/- 0.0208)
depth = 5: CV AUC = 0.5922 (+/- 0.0242)
depth = 6: CV AUC = 0.5941 (+/- 0.0165)
depth = 7: CV AUC = 0.5951 (+/- 0.0219)
depth = 8: CV AUC = 0.5887 (+/- 0.0199)
Best max_depth: 7Note: Decision trees don’t require feature scaling.
Evaluating on Test Data
from sklearn.metrics import accuracy_score, roc_auc_score, classification_report
# Train final models
knn_final = KNeighborsClassifier(n_neighbors=best_k)
knn_final.fit(X_train_scaled, y_train)
tree_final = DecisionTreeClassifier(max_depth=best_depth, random_state=42)
tree_final.fit(X_train, y_train)
# Predictions
y_pred_knn = knn_final.predict(X_test_scaled)
y_pred_tree = tree_final.predict(X_test)
# Probabilities for AUC
y_prob_knn = knn_final.predict_proba(X_test_scaled)[:, 1]
y_prob_tree = tree_final.predict_proba(X_test)[:, 1]
print("k-NN Results:")
print(f" Accuracy: {accuracy_score(y_test, y_pred_knn):.4f}")
print(f" AUC: {roc_auc_score(y_test, y_prob_knn):.4f}")
print("\nDecision Tree Results:")
print(f" Accuracy: {accuracy_score(y_test, y_pred_tree):.4f}")
print(f" AUC: {roc_auc_score(y_test, y_prob_tree):.4f}")k-NN Results:
Accuracy: 0.8212
AUC: 0.6051
Decision Tree Results:
Accuracy: 0.8119
AUC: 0.5956ROC Curves
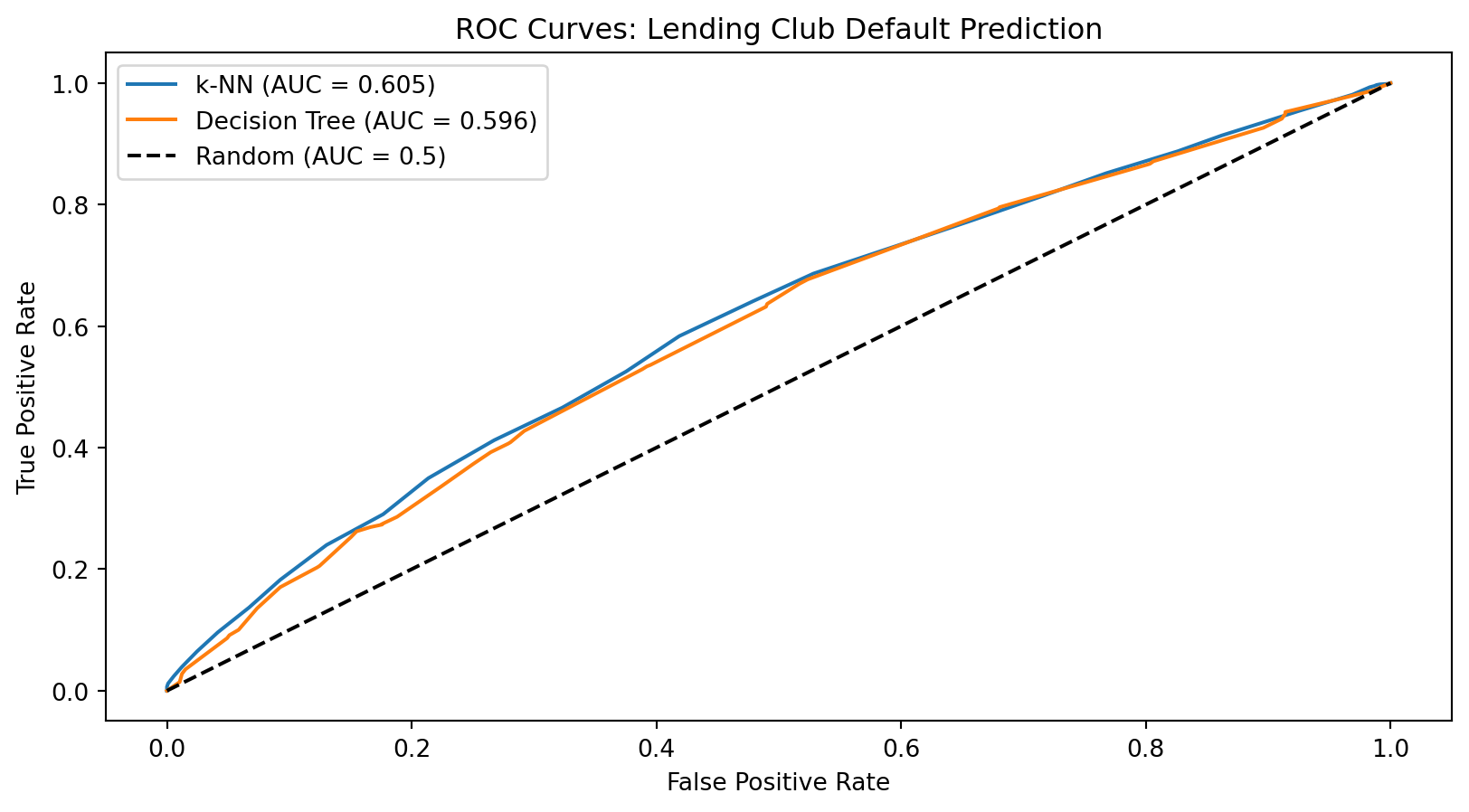
The ROC curve shows the tradeoff between catching defaults (true positive rate) and falsely flagging good loans (false positive rate).
Interpreting the Decision Tree
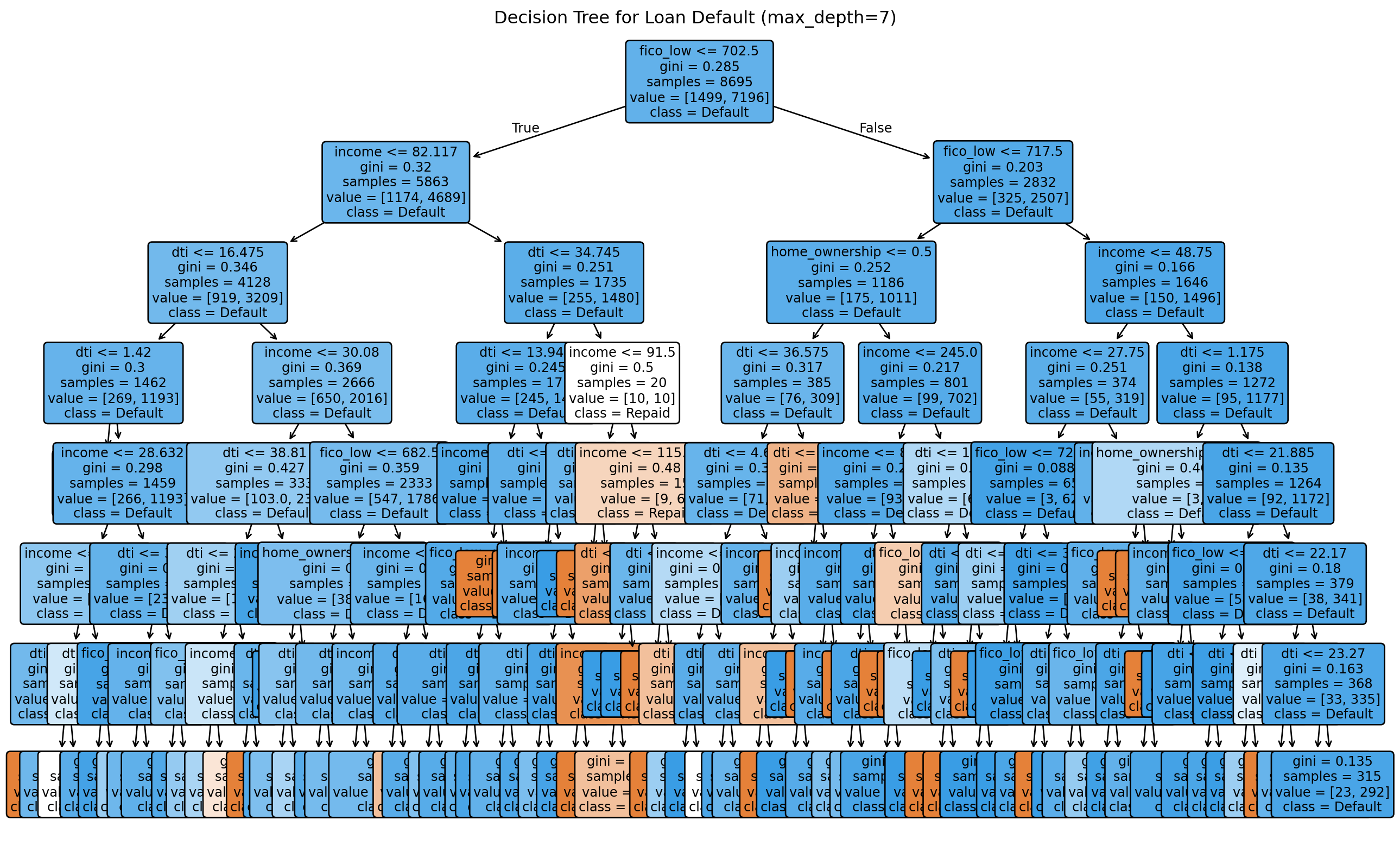
The tree reveals which features matter most. The first split (root) uses the most informative feature—likely FICO score, consistent with banking practice.
Feature Importance
Feature Importances (Decision Tree):
Feature Importance
dti 0.406899
income 0.294622
fico_low 0.256548
home_ownership 0.041931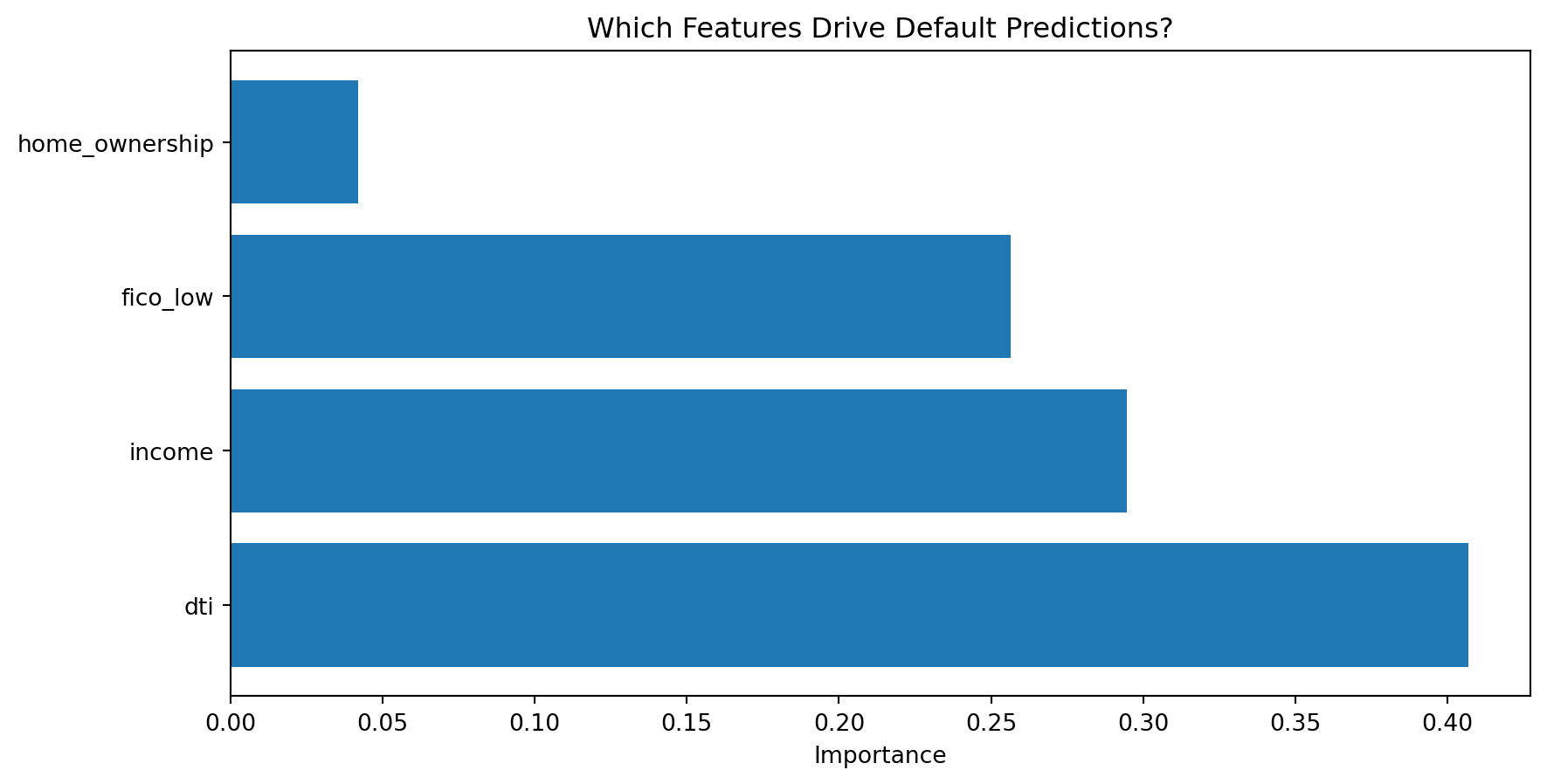
Feature importance tells us which variables the tree relied on most. Higher importance means the feature contributed more to reducing impurity.
Summary and Preview
What We Learned Today
Linear classifiers have limitations: When classes aren’t linearly separable, we need nonlinear methods.
k-Nearest Neighbors:
- Classifies based on majority vote among \(k\) closest training observations
- Creates flexible, curved decision boundaries
- Requires feature scaling; struggles in high dimensions
- No training, but slow at prediction time
Decision Trees:
- Recursively partition data based on feature thresholds
- Creates axis-aligned rectangular boundaries
- Highly interpretable; handles mixed feature types
- Prone to overfitting without regularization
Key Concepts
Information gain measures how much a split improves class purity. Trees greedily select splits that maximize information gain.
Gini impurity and entropy are two ways to measure how mixed the classes are in a node.
Bias-variance tradeoff appears in both methods:
- k-NN: small \(k\) = high variance; large \(k\) = high bias
- Trees: deep trees = high variance; shallow trees = high bias
Cross-validation is essential for selecting hyperparameters (\(k\) or tree depth).
Next Week: Ensemble Methods
Decision trees have high variance—small changes in data can produce very different trees. Next week we’ll see how to fix this.
Week 9: Ensemble Methods
- Random Forests: Average many trees, each trained on random subsets
- Gradient Boosting: Build trees sequentially, each correcting previous errors
- XGBoost: Industrial-strength boosting used in finance and competitions
Ensemble methods combine many weak learners into a strong learner, dramatically reducing variance while maintaining flexibility.
References
- Cover, T., & Hart, P. (1967). Nearest neighbor pattern classification. IEEE Transactions on Information Theory, 13(1), 21-27.
- Breiman, L., Friedman, J., Stone, C. J., & Olshen, R. A. (1984). Classification and Regression Trees. CRC Press.
- Quinlan, J. R. (1986). Induction of decision trees. Machine Learning, 1(1), 81-106.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning (2nd ed.). Springer. Chapters 9, 13.
